
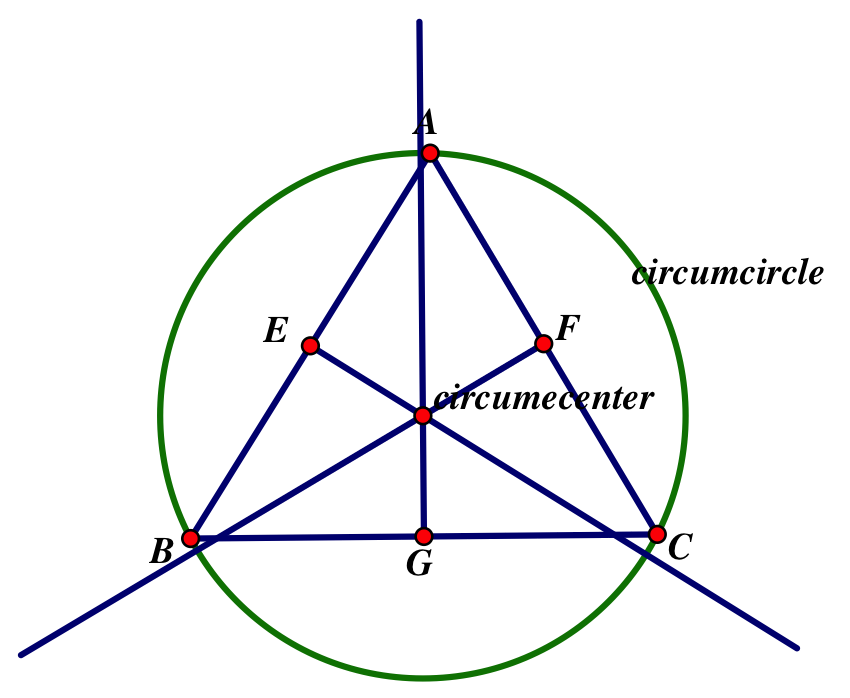
Squares and Rectangles Inscribed in Circles So even if you don’t see the right angle marked, you can rest assured the inscribed angle at that third vertex is 90 degrees. And a key thing to note: an inscribed triangle will ALWAYS be a right triangle. Inscribed TrianglesĪn inscribed triangle is any triangle with a circle’s diameter as one of its sides and a vertex along the circumference.
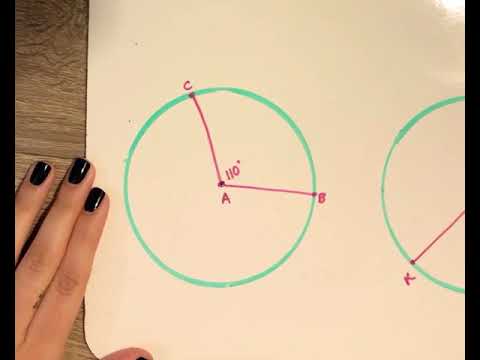
So any triangle with the center of the circle as one vertex and points along the circumference as the other two vertices will automatically be an isosceles triangle. Remember that the two angles opposite those two sides are also of equal measure. Since two side are of equal length, the triangle is automatically isosceles. What does that guarantee about the triangle? In this case, notice that two of the sides of the triangle are radii (remember, a radius is any line segment from the center of the circle to its circumference). This can manifest itself in three common ways: Triangles Created Using the Central Angle of a Circle (For clarification, the diagonal of a rectangle is a bisector when the rectangle is a square, but it is not a bisector in any other case.)Īnother very common combination of shapes in more difficult GMAT Geometry problems is triangles with circles. This makes sense when you think about it, because the diagonal bisects two 90-degree angles to give you two 45-degree angles:
You’ve probably seen a rectangle split in two along one of its diagonals to produce two right triangles:īut one of the oft-overlooked basic geometric truths is that when that rectangle is a square (and yes, remember a square is a type of rectangle), the diagonal splits the square into two isosceles right triangles. Today, we’ll talk about some crucial connections that are often made between triangles and other figures, starting with the 45-45-90 triangle, also known as the isosceles right triangle. Here are just a few examples, which include triangles within and outside of squares, rectangles, and circles: As discussed before, now that we’ve talked about the basic triangles, we can start looking at how the GMAT can make problems difficult by embedding triangles in other figures, or vice versa.


 0 kommentar(er)
0 kommentar(er)
